Help

Before talking about symmetry, let's start with the more familiar situation of quantifying amount. A typical question we might pose to a very young child is "which pile has more marbles?"

Versions of this question can be answered by even animals such as birds. No specialized language is required to make qualitative comparisons on the level or "more" or "less." But we have developed the language of the positive integers to enable ourselves to answer such questions more precisely. Rather than simply saying the righthand pile has more marbles, we can say it has three more marbles because the lefthand pile has four marbles and the righthand pile has seven marbles.

Returning to symmetry, we can ask an analogous question in regards to the below three images: "Which image has the most symmetry?"

It's less obvious what to say here. Some people might propose the righthand picture has "less" symmetry (whatever that means), but few are likely to be able to immediately say much more than that. While we are taught numbers in school to help us quantify amounts, a specialized language for symmetry is not part of a standard US education. One goal of this help page is to give you a short introduction to this language. (For details on how to use SymmetryCat, see this page.) To this end, let's return for a moment to counting.

Using numbers, we learn at an early age to recognize that the left and right groups above are equivalent in both having three elements while the middle group is different in that it has four elements. We end up with an abstract notion of "three" or "three-ness." Whenever we see a pile of objects we can decide whether or not it has this "three-ness" property in the same way we can look at any object and decide whether it has the property of "blue-ness."

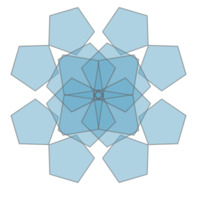
It turns out there is a mathematical language for quantifying symmetry that is analogous to the way in which the language of the integers quantifies amount. This language of symmetry will, for example, define a property called "pgg symmetry." For any image, we will be able to decide whether or not it has this property. Just as every pile of objects can be labeled with "three-ness" or "five-ness" or "112-ness" or ..., we'll be able to label any image with a particular type of symmetry. For example, the left and middle images below have the same amount of symmetry — namely, "p4g symmetry" — while the right image has a different amount of symmetry, "pgg symmetry"

As discussed in the next section, the approach that has been taken in mathematics for quantifying symmetry is to focus on what geometric transformations leave the original image/object unchanged. What is perhaps surprising is that in some quite general situations, there are only a finite number of collections of transformations we can end up with. For example, for "wallpaper patterns" discussed below there are exactly 17 possibilities: p4g, pgg and fifteen others. It's not obvious from the outset that there are only a finite number of possibilities. It's certainly not the case when talking about quantity!

Before getting to various types of symmetry such as "pgg symmetry," we need to be a little more precise about what we mean by "symmetry." We will then be able to introduce some atomic types of symmetries that we can combine in a certain sense to yield these more advanced concepts.

For concreteness, let's assume we have image we're interested in. A symmetry of the image is a "transformation" that leaves it looking unchanged. The ones we will consider are the Euclidean plane isometries. This will all become clearer in a moment as we see some examples!

Rotational symmetry

One simple case is when the image/object can be rotated a certain amount without changing its appearance. For example, if we rotate the middle image below by 72 degrees (one fifth of a full rotation) counterclockwise, the image is left unchanged. We say that "a rotation of 72 degrees counterclockwise" is a (rotational) symmetry of the middle image.

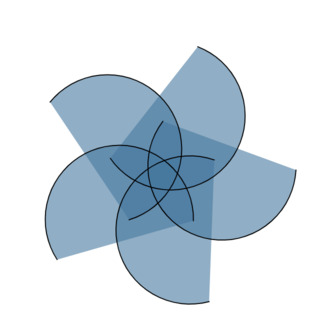
Having a specific rotational symmetry generally provides additional rotational symmetries as well. Take the middle image again. As mentioned above, rotating it one fifth of a full revolution leaves it unchanged. It follows that we can rotate it another one fifth and still have an image that matches the original. But then we could have rotated "twice 72 degrees," or 144 degrees, right from the start. In fact, any multiple of 72 degrees works.

Given a rotation R, we'll write R² for the rotation applied twice, R³ for the rotation applied three times, etc. Continuing the example from above, if R is our 72-degree counterclockwise rotation, then R² denotes 144 degrees counterclockwise, R³ denotes 216 degrees counterclockwise and R⁴ denotes 288 degrees counterclockwise. R⁵ — a rotation of 360 degrees — returns the image to its original orientation. We can continue with R⁶, R⁷, etc. but these symmetries are redundant with ones we're mentioned.

Principle: If a rotation R is a symmetry of an image, then so is Rⁿ for any positive integer n.

It's often convenient to identify the smallest rotation that is a symmetry of an image. In the above three cases, these are rotations of 180, 72 and 20 degrees, respectively.

Note: To specify a rotation you must specify both an amount you are rotating by as well as the point about which the rotation is being made. In the above discussion it's implicit that each rotation is about the center of the image. With some of the images we'll see later on we will need to be more careful about this issue and will specify the points of rotation explicitly.

The identity symmetry

Now that we've seen rotations, it's a good time to mention that the transformation that "does nothing" is also an isometry. If you'd like, you can think of this as a rotation by zero degrees.

Note:We won't need to concern ourselves with the identity symmetry, but it becomes important when you delve into the mathematics more rigorously. In such a case, it becomes useful to be able to associate at least one symmetry to every image, even one such as the below.

Reflectional symmetry

We are all familiar with the bilateral symmetry of humans and many animals. We can view this geometrically as an example of a reflectional symmetry. With rotational symmetries there is an implicit "center" of rotation. For reflections we need a reflection axis (i.e., line) about which we are reflecting.

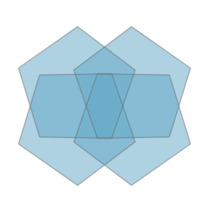
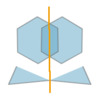
The below three images have one, two, and four reflectional symmetries, respectively.

Here are the same three images as above, but with the lines of reflection marked explitly in orange.

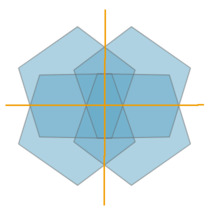
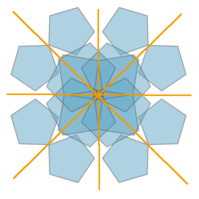
Note: The second and third images above have both rotational and reflectional symmetries (the middle image can be rotated 180 degrees; the right image can be rotated 90 degrees). They are said to have dihedral symmetry.

Translational symmetry

A fourth type of symmetry arises from translational symmetries. For example, in the below image, sliding everything over to the right (or left) by certain amounts leaves the string of images unchanged. Just as with rotations, if we let T denote a given translation, then multiple applications of this translation (e.g., T³ for the translation applied three times) are also symmetries. Note that for any of this to work, we need the images to continue indefinitely to both the left and the right, but this is a simply a matter of imagination. It's common to consider idealized situations where patterns continue indefinitely.

In the above picture, all possible translations lie along a single line: We can either translate to the right or to the left. Sometimes, however, there are translations in two "independent" directions. This is the case for the below image in which representative translations are shown.

Convention: We frequently have to imagine that the image continues beyond what is shown for the symmetry to work.

Glide symmetry

It will be convenient to consider one final class of symmetries known as the glide reflections. A glide reflection can be thought of as a translation followed by reflection (through the same axis we just translated along). A representative glide reflection is shown below: The orange arrow indicates the magnitude of the direction of the translation and also serves as the line of reflection for the subsequent reflection.

Notice that if we denote a glide reflection by G, then G² is a translation since we have reflected about the same axis twice.

• 2D discrete point groups: No translational symmetries

  These are the symmetry groups that arise when there are no translations. The possibilities can be divided into two categories:

  • Rotations only. If a rotation of 360/n degrees can be made, then the image is said to have C_n symmetry. (Here the "C" stands for "cyclic.") So we have the possibilities C₁, C₂, C₃, etc. C₁ indicates there are no rotations all that work other than going around a complete 360 degrees.
  • Rotations and reflections. If there is a reflectional symmetry and a rotation of 360/n degrees is the smallest rotation that can be made, then the image is said to have D_2n symmetry. (Here the "D" stands for "dihedral.") When n is at least 3, D_n embodies the symmetries associated a regular n-gon. D₁ is the special case in which the only symmetry is a single reflection. D₂ is the collection of symmetries associated to a non-square rectangle.
• Frieze groups: "One-dimensional" symmetries

  These are "one-dimensional" symmetries in which there is at least one translational symmetry, but for which all translational symmetries are paralllel. Images with symmetries encoded by a frieze group consist of a pattern repeated along an infinite line.

  Let's let T denote the shortest translation to the right that leaves the image unchanged. Any reflection is going to have to leave this translation line unchanged, so any reflection has to be about a vertical line or about a horizontal line coinciding with the translation axis. Similarly, any glide reflection will have to share an axis with the translation axis as well and any rotation will have to be of 180 degrees. Naively, this leads to a categorization of 2*2*2*2=16 possible collections of symmetry. It turns out that only 7 combinations can be realized. We won't go through the proof here, but it boils down to the fact that there are relations among the different types of symmetry. For example, reflecting about a vertical axis and then above a horizontal axis results in a 180-degree rotation. So it's not possible to have an image with both vertical and horizontal reflections and no rotations.

  The reader might wonder about the possibilities for "where" any rotations or reflections about vertical axes appear. It turns out that because of the translational symmetry, if there is even one vertical reflection, thene there are an infinite number, one for each "unit cell."

  The 7 classes along with examples of each. For now I link to wikipedia's table

• Wallpaper groups: "Two-dimensional symmetries"

  These symmetries arise for images in which there are at least two translations that are not parallel. The name arises from the fact that many tradiational home wallpapers have patterns with such symmetries.

  It is a theorem that there are exactly 17 possibilities in this class. This is amazing! It's not obvious that there wouldn't be an infinite number of classes.

  The simplest, called p1, occurs when there are no symmetries other than the ones generated by the two independent translations. At the other end of the spectrum, an image with p6m symmetry is invariant under certain rotations by 60 degrees as well as under a number of reflections and glide transformations. Below we give examples of each type.

  The 17 classes with examples. For now I link to wikipedia's table. Eventually I would like to add something a little less complicated.

Note: We are only considering images satisfying a certain discreteness condition. Roughly, this means there aren't "arbitrarily small" rotations or translations. Assuming this condition means we don't have to consider an images such as a single circle (arbitrary rotations), an infinite line (arbitrary translations) or a uniform plane (arbitrary rotations and translations).