Help
Think of it as iNaturalist but for symmetry instead of for species.
What can you do on SymmetryCat?
SymmetryCat is designed to let you upload pictures and classify them according to their symmetry. You may view images that others have uploaded without logging in, but to upload your own images, you should first Sign up and then Log in. Once you have that settled, you can- Upload your own image and then annotate and classify it (wallpaper only right now)
- View images you or others have uploaded
- Edit your profile
- The ability to filter observations by various properties (e.g., symmetry class, who uploaded, location, ...)
- Add point-group and frieze pattern symmetries to classifier
- Tag images (e.g., by object, by school class, ...)
- Statistics regarding percentage of uploaded images falling into various symmetry classes.
Guide to how to annotate an image and classify it
From the listing for a given observation, click on the "classify" link to allow you to annotate the image as to what the rotational, reflectional, translational, and glide symmetries are and then select a specific symmetry class.
General notes on classifying
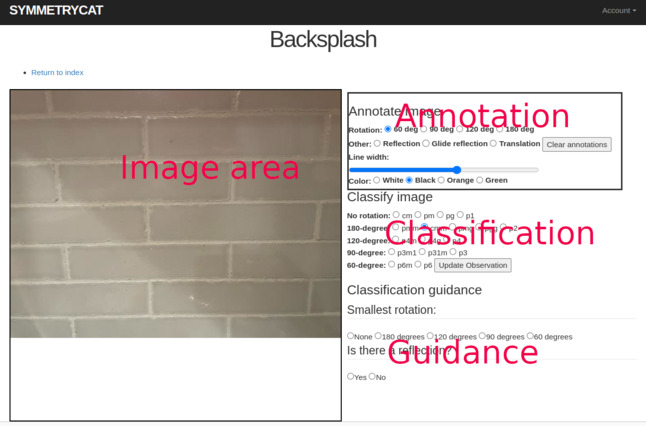
At the moment, the classification page has four main areas.
-
Image area
This is where you should actually draw on the image to indicate specific symmetries. -
Annotation area
Here you can select what type of annotation you wish to add. The color should be chosen so as to contrast with the background of the image — the color does not have any meaning as to what kind of symmetry is being marked. Unfortunately, "Clear annotations" currently removes all annotations. This should be fixed soon!
When annotating:
- If a rotation is selected, clicking at any point in the image will add a marker designating a rotation. The shape of the marker indicates the number of degrees.
- If a translation, reflection or glide is selected, you must click twice to mark two points of the line. At this point, nothing displays after the first click, but the line will show up after the second click. The style of the line indicates which type of symmetry is denotes.
- By the vary nature of these images, a given symmetry will typically repeat many times in the image. We recommend marking it once, close to the center of the image.
-
Classification area
After annotating your image and following the flowchart guidance, select the appropriate symmetry class. Then click the update button to save your modifications.
-
Guidance area
Here flowchart logic is encoded to guide you to the correct classification. We recommend you look at this after annotating your image. Once the minimum rotational symmetry has been selected and you have answered whether or not there are any reflectional symmetries, further guidance will be displayed.
Example classification
Here we illustrate the process of determining the symmetry class for a particular image. We have highlighted in red the central hexagon. Note that it is not regular, the smallest rotation that will be a symmetry is 180 degrees. Similarly, this implies that the only reflections (as we see marked below) are vertical and horizontal.

In the second image we have marked representative rotations of 180 degrees. Note that there essentially three different points we can rotate about. In general we recommend only marking minimal rotations. So, for example, if there are rotational symmetries of 90 degrees, don't bother marking any of 180 degrees.

In the third image we have marked in green two reflectional symmetries. In white we have marked a glide reflection.

We have opted not to mark any translational symmetries as it doesn't really help with the classification. In the image below we show the appropriate selections for the two guidance questions. The minimal rotation is 180 degrees and there are rotations in two directions. We see that there is a rotation about a point not lying on a reflection axis, so the symmetry class is pmm.
